Matlab Questions:
please answer all of the questions below and explain it, I will rate the answer thank you!
![Solved: please answer all of the questions below and explain it, I will rate the answer thank you! 1 Page IV: Questions 29-32: Recursion The following is a recursive Matlab function, function [out] =midtermRec (n) if le (n,2) out = 1 elseif eq(n,3) out = 2 else + midtermRec (n-3) out = midtermRec (n-1 ) end end 29. (1 point) What will be value assigned to out by the command >> out- midtermRec (1)? a. C. d. 3 30. (1 point) What will be the value assigned to out by the command >> out midtermRec (4) a. b. 3 C. 4 d. 6](https://d2vlcm61l7u1fs.cloudfront.net/media%2F712%2F7120f903-e6de-41bb-9417-0f036b1041bc%2FphpBCyxLy.png)




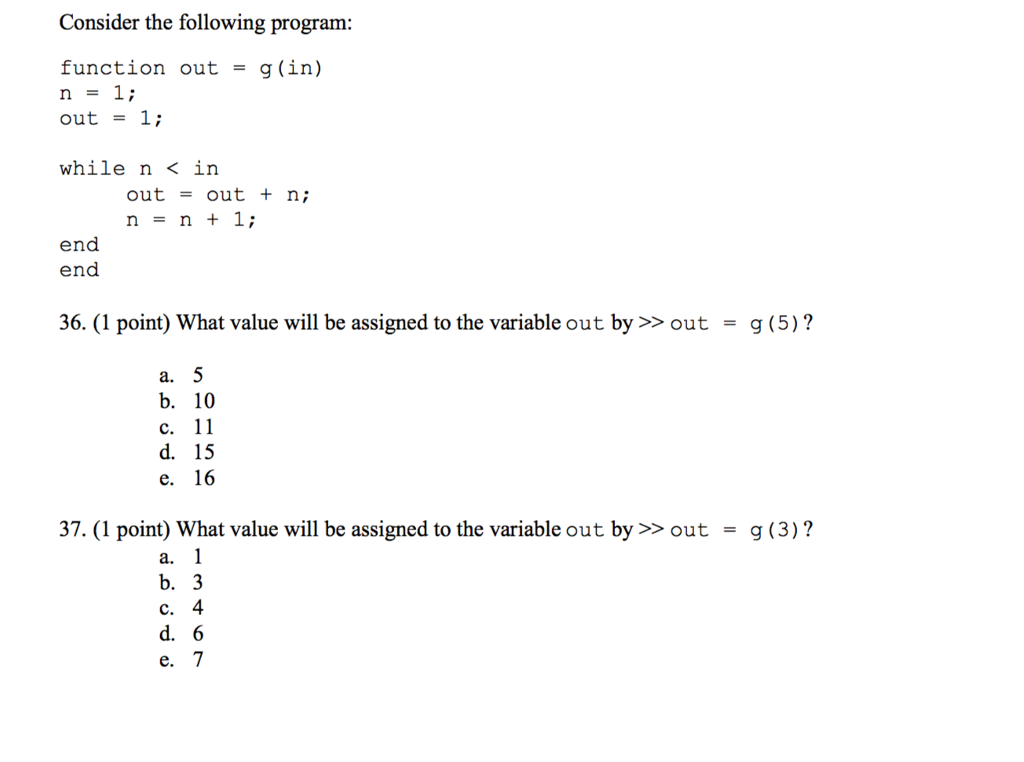
Show transcribed image textPage IV: Questions 29-32: Recursion The following is a recursive Matlab function, function [out] =midtermRec (n) if le (n,2) out = 1 elseif eq(n,3) out = 2 else + midtermRec (n-3) out = midtermRec (n-1 ) end end 29. (1 point) What will be value assigned to out by the command >> out- midtermRec (1)? a. C. d. 3 30. (1 point) What will be the value assigned to out by the command >> out midtermRec (4) a. b. 3 C. 4 d. 6
Expert Answer
function [out] = midtermRec(n) %determine function of midtermRec with n param
if le(n,2) % it will check whether the value n is less than or equal to 2, if so then the out value is 1.
out = 1
elseif eq(n,3) %if n is equal to 3 then the out value is 2
out = 2
else % otherwise then out value is sum of the recursion function
out = midtermRec(n-1)+midtermRec(n-3)
end
end
29.midtermRec(1)
The answer is b.1 . Since the n value is 1. So it is true for if le(n,2) case.
30.midtermRec(4)
The answer is b.3
in this case it is false for both if le(n,2) and elseif eq(n,3) case. So it goes to out = midtermRec(n-1)+midtermRec(n-3).
midtermRec(n-1) => midtermRec(3) => here n is 4 so n-1 is 3.call function again using recursion method.
midtermRec(3) this will return the out value is 2. (elseif eq(n,3) out = 2)
then consider midtermRec(n-3),
midtermRec(n-3) => midtermRec(1) => here n is 4 so n-3 is 1. call function again using recursion method.
midtermRec(1) this will return the out value is 1. (if le(n,2) out = 1)
finally add 2 values like out = midtermRec(n-1)+midtermRec(n-3) => out = 2+1, so out=3
31.midtermRec(5);
The answer is d.2,1,3,1,4
midtermRec(5) in this case for both if le(n,2) and elseif eq(n,3) case. So it goes to out = midtermRec(n-1)+midtermRec(n-3).
midtermRec(n-1) => midtermRec(4) => here n is 5 and n-1 is 4. so it will call again midtermRec(4).
midtermRec(4) => in this case for both if le(n,2) and elseif eq(n,3) case. So it goes to out = midtermRec(n-1)+midtermRec(n-3).
midtermRec(n-1) => midtermRec(3) => here n is 4 so n-1 is 3.call function again using recursion method.
midtermRec(3) this will return the out value is 2. (elseif eq(n,3) out = 2)
so first it will print 2
then consider midtermRec(n-3),
midtermRec(n-3) => midtermRec(1) => here n is 4 so n-3 is 1. call function again using recursion method.
midtermRec(1) this will return the out value is 1. (if le(n,2) out = 1)
so second it will print 1
finally add 2 values like out = midtermRec(n-1)+midtermRec(n-3) => out = 2+1, so out=3
and then 3rd it will print as 3
midtermRec(n-3) => midtermRec(2) => here n is 5 and n-1 is 2.
In this case if le(n,2) is true so the out value is 1.
so 4th it will print as 1.
finally add midtermRec(4) + midtermRec(2) from previous case, so 3+1 => 4. So 5th it will print as 4.
32. The answer is c.function y = myFun(n)
if n==1
y=1
else
y=myFun(n-1)+n^2
end
end
consider myFun(5)
false for if n==1 so it will move to else part. here there is a function call of myFun(n-1)
y = 1
y = 5
y = 14
y = 30
y = 55 hence 55 will be returned
as per equation y(n) = n^2+(n-1)^2+(n-2)^2+…+2^2+1,
if replace n=5
y(5) = 5^2+(5-1)^2+(5-2)^2+…+2^2+1
=> 25+16+9+4+1
it will return 55 as y value.

