In class we calculated the LCOE (or bid price) for a power plant with the following parameters:
Overnight cost of $10 billion
Lifetime of 30 years
Annual output of 8.64 million MWh
Marginal cost of $20/MWh (so total operating costs per year are $20/MWh ´ 8.64 million MWh = $172.8 million per year)
Discount rate of 5%
Re-calculate the LCOE with the following additional information:
The plant faces a tax rate of 34%
The plant must maintain a fuel inventory valued at $20 million, beginning in Year 0. This inventory is liquidated at face value ($20 million) at the end of the plant’s lifetime.
Capital costs are depreciated via straight-line depreciation over the life of the plant.
The plant has no salvage value and there are no other working capital requirements.
Remember to use the correct units in your answer for LCOE ($/MWh).
Expert Answer
Levelized Cost of Energy (LCOE) is calculated by dividing the total cost of the project (net of benefits) by the total power produced over the life of the plant
Overnight cost of Project ($Million) = 10Billion x 1000 = $10,000MM
Depreciation (straight line) is calculated by dividing the cost i.e. $10,000MM by the life (30 years) = $333.3333MM per year
Tax savings on Depreciation = $333.3333MM x 34% = $113.3333MM per year
The table below computes the present value of the annual cash flows
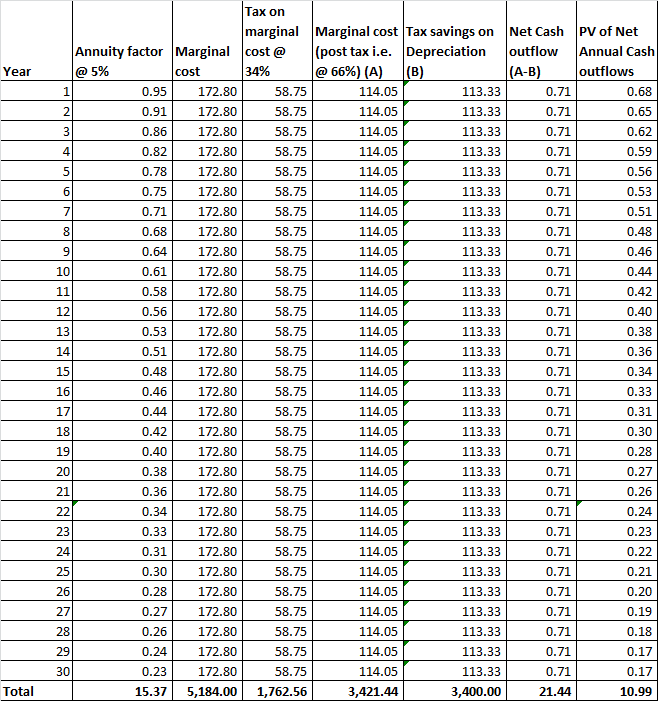
Hence the Present value of the annual cash outflows is $10.99MM
(An alternate method of computing the Present value of the cash flows is to multiply the annual cash flows with the sum of Annuity @ 5% = $0,71MM x 15.37 = $10.99MM)
Present value of Liquidation of Inventory = $20MM x discounting factor at 30th year = $20MM x 0.23 = $4.63MM
Net present value of Inventory cost = $20MM – $4.63MM = $15.37MM
Total cost over the life of the project = $10,000MM + $10.99MM + $15.37MM = $10026.36MM
Total output over 30 years = 8.64MM MWh x 30 years = 259.2MM MWh
LCOE = $10026.36MM / 259MM MWh = $38.68 per MWh

